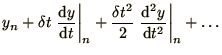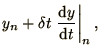Next: Stability
Up: Euler Method
Previous: Euler Method
Order of Accuracy
How accurate is the Euler method? To quantify this we consider a Taylor
expansion of 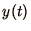 around
around 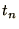
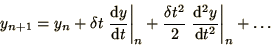 |
(1.14) |
and substitute this into (1.11)
where we have used (1.7) to obtain the final form.
Hence, we see that the term in 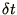 in the expansion has been
correctly reproduced by the approximation, but that the higher order
terms are wrong. We therefore describe the Euler method as 1st
order accurate.
An approximation to a quantity is
in the expansion has been
correctly reproduced by the approximation, but that the higher order
terms are wrong. We therefore describe the Euler method as 1st
order accurate.
An approximation to a quantity is 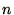 th order accurate if the term in
th order accurate if the term in 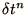 in the
Taylor expansion of the quantity is correctly reproduced.
The order of accuracy of a method is the order of accuracy
with which the unknown is approximated.
Note that the term accuracy has a slightly different meaning in
this context from that which you might use to describe the results of an
experiment. Sometimes the term order of accuracy is used to
avoid any ambiguity.
The leading order deviation is called the truncation error. Thus
in (1.2.1) the truncation error is the term in
in the
Taylor expansion of the quantity is correctly reproduced.
The order of accuracy of a method is the order of accuracy
with which the unknown is approximated.
Note that the term accuracy has a slightly different meaning in
this context from that which you might use to describe the results of an
experiment. Sometimes the term order of accuracy is used to
avoid any ambiguity.
The leading order deviation is called the truncation error. Thus
in (1.2.1) the truncation error is the term in 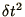 .
.



Next: Stability
Up: Euler Method
Previous: Euler Method